Figure. Examples of the results derived by Aalto University’s computer simulation approaches: Magnetohydrodynamic (MHD), hybrid, and full kinetic electrostatic and electromagnetic approaches.

In parallel to space remote and in-situ observatories, physical models have been developed to account for the observations and to predict the state of the space environment of the solar system objects. Several descriptions have been historically used, which are complementary: kinetic, fluid and hybrid. They are obtained by extending the kinetic theory of gases (see Boltzmann formalism) and the hydrodynamics of fluids to the plasma state of matter. The choice of the plasma description, either kinetic, hybrid or fluid, is intimately determined by the characteristic temporal and spatial scales encountered in the environment of study. This remark is illustrated in Illustration 3 when looking at the characteristic frequencies of the plasma, i.e., electron plasma frequency ω_pe, ion plasma frequency ω_pi, ion gyrofrequency ω_ci, Alfvén frequency ω_a, and electron-ion collision frequency ω_ei.

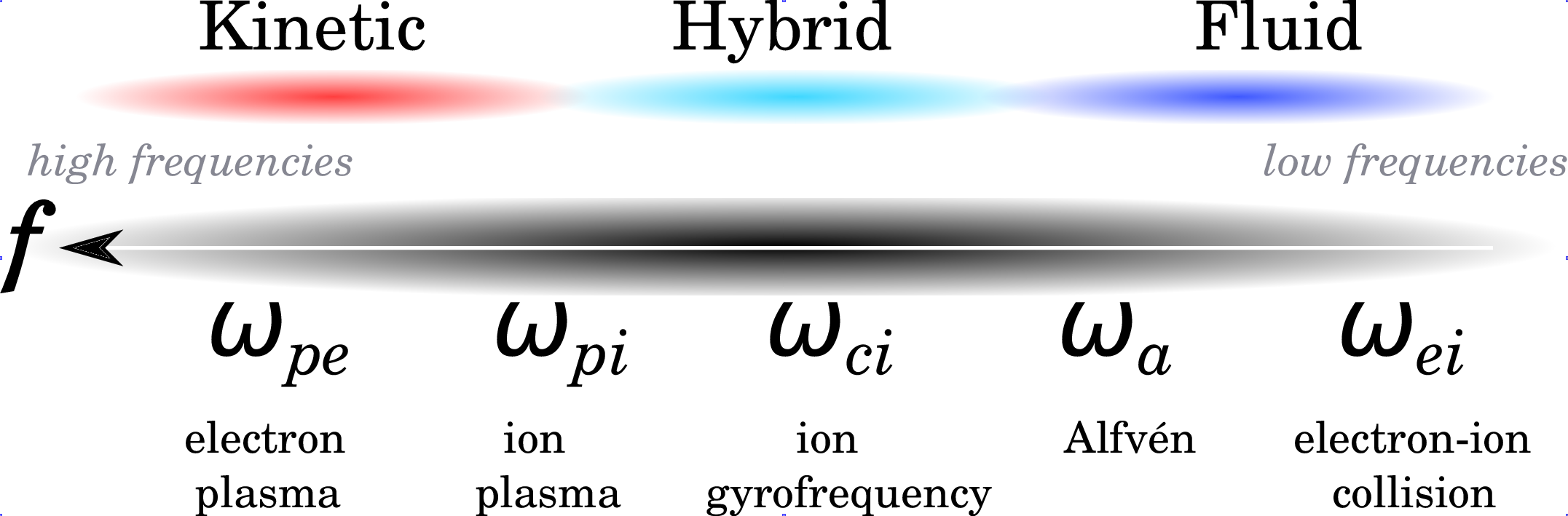
There are three basic self-consistent approaches to describe space plasmas: (a) kinetic, (b) hybrid and (c) fluid approaches:

(a) Kinetic description:

The most fundamental description of plasma is the kinetic one where the position of particles is known in phase space, that is the space of all possible values of position and momentum variables. In the kinetic description, even the electron scale is accessible. Two different kinds of approaches may be used: [1] based on a distribution function and [2] based on individual (macro) ions. In case [1], the microscopic distribution function f in 6 dimensions (3 of space, 3 of velocity) represents all there is to know about the plasma state: in other words, f is the number of particles per unit volume having a given velocity at a certain time. The evolution of the plasma is most generally described by the Boltzmann dissipative equation, introduced by Ludwig Boltzmann in 1872. These kinetic models aim at precisely solving this equation. Macroscopic quantities such as number density, velocity, energy and heat transfer can be accessed by integrating the distribution function over velocity space. In the other approach [2] particles are modelled as “macro particles” or “particle clouds” which are accelerated by the Lorentz force, gravitational force, etc. Because kinetic simulations are computationally extremely demanding, most kinetic models are restrained to 1D studies. The HYB-em Particle-In-Cell (PIC) electromagnetic model developed at Aalto, based on the HYB-* platform but considering both electrons and ions as particles, is one such full kinetic model.

(b) Hybrid kinetic/fluid description:

Hybrid models adopt the standpoint where ions are seen as particles and electrons become a massless fluid. The advantage of such a method is that the small-scale physics of ions is more accurately described since no assumption on the form of their distribution function is made. One of the main caveats of hybrid models is that they require a large number of particles to reach statistically significant results. Thanks to increasing computational resources, hybrid models have become more and more popular over the last 10 years. The HYB-* platform developed at Aalto belongs to this category and is described in more detail below.

(c) Fluid description:

This description refers to any simplified plasma model that deals with quantities averaged over velocity space, hence, necessarily, with macroscopic quantities. Introduced by Hannes Alfvén as soon as 1942 in its ideal form, magnetohydrodynamics (MHD) assumes that the plasma behaves as a fluid embedded in its magnetic field upon which the Lorentz force acts. One shortcoming of this approach is that it implicitly assumes that the plasma is collisional with particle distributions having Maxwellian distributions, a condition which, in practice, is not met for smaller scale structures. The advantage of the MHD approach is that it is computationally much less expensive than kinetic and hybrid approaches and, therefore, it provides the possibility to obtain a good spatial resolution as well as to model large space regions.

Further reading:

Review of available models and approaches:

Kallio, E., J-Y Chaufray, R. Modolo, D. Snowden and R. Winglee, Modeling of Venus, Mars, and Titan, Space Science Reviews, DOI 10.1007/s11214-011-9814-8, 2011.

Distinction between Kinetic, Hybrid and Fluid plasma models, and introduction to kinetic simulations with differences in the modelled physics:

Winske, D., and N. Omidi (1996), A nonspecialist's guide to kinetic simulations of space plasmas, J. Geophys. Res., 101(A8), 17287–17303, doi:10.1029/96JA00982.

General textbooks about numerical simulations in plasma physics:

C. K. Birdsall and A. B. Langdon, Plasma physics via computer simulation, Series in Plasma Physics, Taylor & Francis Ltd, New York, 2004, ISBN 9780750310253.

R. W. Hockney, J. W. Eastwood, Computer Simulation Using Particles, McGraw-Hill, New York, 1981, ISBN 9780852743928.