The Physics of the HYB-* model

We currently develop hybrid and kinetic plasma simulations dedicated to planetary plasma interactions. These platforms are developed for the interactions between non-magnetized or weakly magnetized Solar System bodies and the plasma flow such as the solar wind.

In the hybrid approach ions are treated self-consistently as particles moving in an electromnagnetic fields and electrons are modelled as a charge-neutralizing fluid.

The HWA/HYB-* platform, now at Aalto University after being originally developed at FMI (Helsinki, Finland), has been used to study the solar wind interactions of several objects such as Mercury, Venus, the Moon, Mars, Ceres, Pluto and, more recently, comets. The platform has also been used to study the interaction of Titan with Saturn's magnetospheric plasma and magnetic field. Kinetic modelling within HYB-* has been applied to the lunar plasma and dust environment. Details of the HYB-* hybrid simulation model are described, for example, in Kallio & Janhunen (2003) or at the FMI web page.

The Quasi-Neutral Hybrid model

The HYB simulation code is originally based on the quasi-neutral hybrid (QNH) description of plasma. Positively charged ions are treated explicitly as kinetic particles and electrons are modelled as a charge-neutralizing, massless MHD fluid. The ions and the electromagnetic fields are self-consistently coupled to each other. The implicit treatment of electrons by the fluid momentum equation defines the electric field. Physical laws that define the QNH model are the following:

• The dynamics of the ions in the electromagnetic field is governed by the Lorentz force:
  
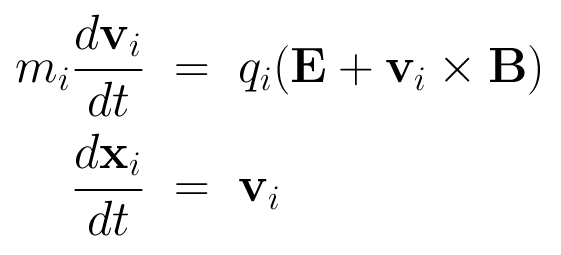
• The electrons are considered implicitly as an inertia-less fluid by the fluid momentum equation:
  
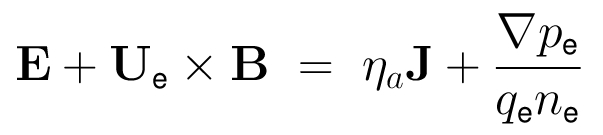
• The ideal gas law as the electron equation of state is:
  
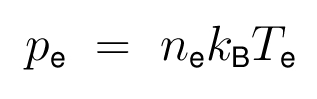
• The quasi-neutrality condition of the plasma is:
  
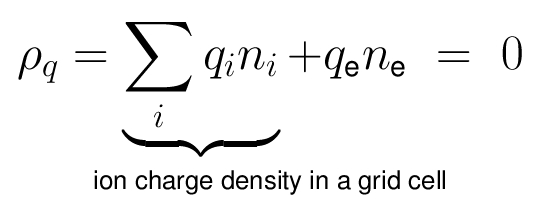
• The electric current density is defined as:
  
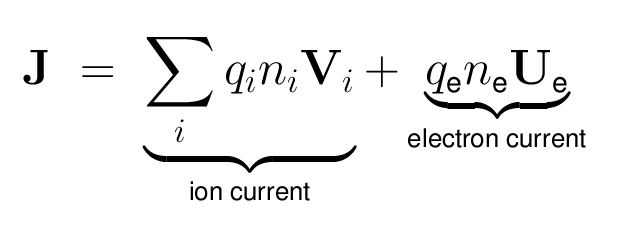
• Electrodynamics comes from the non-radiative Maxwell equations:
  

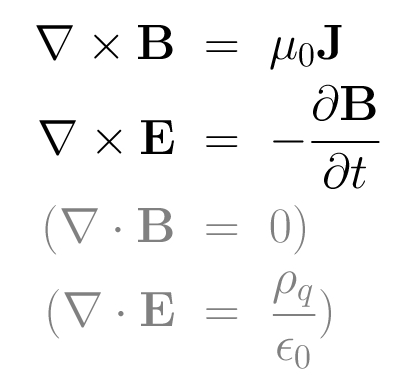
Summary

Assumptions:

• Quasi-neutrality
• Maxwell's equations solved consistently
• Ions accelerated by the Lorentz force and gravitation
• Magnetic field propagated using Faraday's law

Physical inputs:

• Object: Diameter and mass of the planet, gravity, intrinsic magnetic field, atmosphere & ionosphere, electric conductivity
• Flowing plasma (e.g., the solar wind): Density of ions, velocity distribution of ions, electron temperature, the ambient magnetic field (e.g., the Interplanetary magnetic field, IMF)

Solving the hybrid model

Example of the HYB-* platform: step-by-step

Equations of the QNH HYB model are solved by starting with initial values for the ions (positions and velocities) and the magnetic field in the simulation domain.

1. The current density is obtained from the magnetic field by Ampère's law
2. The electron charge density comes from the quasi-neutrality assumption in a grid cell
3. The velocity field of the electron fluid is determined from the definition of the current density
4. The electric field is calculated from the electron momentum equation
5. Magnetic field is advanced by the Faraday's law
6. Particles are moved and accelerated by the Lorentz force

Numerical solution: solving the hybrid model equations

Numerical approaches that are chosen which may differ from one model to another.

HWA/HYB-* model

The HWA/HYB-* platform is described in great technical detail in Kallio and Janhunen (2003):
Kallio E. and P. Janhunen, Modelling the Solar Wind Interaction With Mercury by a Quasineutral Hybrid Model, Ann. Geophys., 21(11), 2133-2145, doi:10.5194/angeo-21-2133-2003, 2003